How to learn stably: H-term¶
Stability plays a key role in productizing DRL applications to real-world problems, making it a central concern of DRL researchers and practitioners. Recently, a lot of algorithms and open-source software have been developed to address this challenge. A popular open-source library Stable-Baselines3 offers a set of reliable implementations of DRL algorithms that match prior results.
In this article, we introduce a Hamiltonian-term (H-term), a generic add-on in ElegantRL that can be applied to existing model-free DRL algorithms. The H-term essentially trades computing power for stability.
Basic Idea¶
In a standard RL problem, a decision-making process can be modeled as a Markov Decision Process (MDP). The Bellman equation gives the optimality condition for MDP problems:

The above equation is inherently recursive, so we expand it as follows:

In practice, we aim to find a policy that maximizes the Q-value. By taking a variational approach, we can rewrite the Bellman equation into a Hamiltonian equation. Our goal then is transformed to find a policy that minimizes the energy of a system. (Check our paper for details).
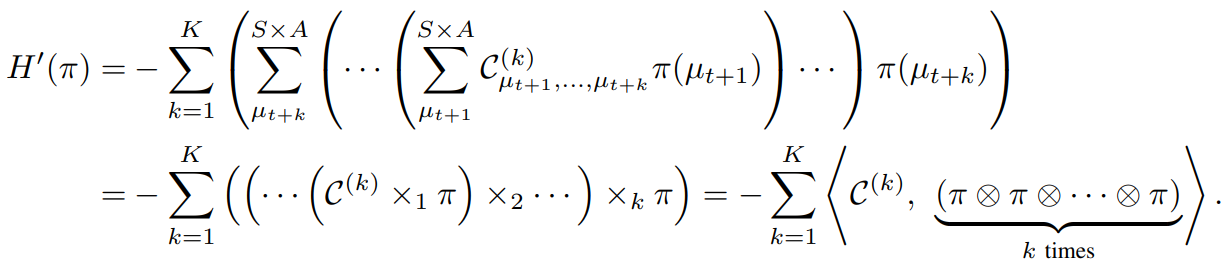
A Simple Add-on¶
The derivations and physical interpretations may be a little bit scary, however, the actual implementation of the H-term is super simple. Here, we present the pseudocode and make a comparison (marked in red) to the Actor-Critic algorithms:

As marked out in lines 19–20, we include an additional update of the policy network, in order to minimize the H-term. Different from most algorithms that optimize on a single step (batch of transitions), we emphasize the importance of the sequential information from a trajectory (batch of trajectories).
It is a fact that optimizing the H-term is compute-intensive, controlled by the hyper-parameter L (the number of selected trajectories) and K (the length of each trajectory). Fortunately, ElegantRL fully supports parallel computing from a single GPU to hundreds of GPUs, which provides the opportunity to trade computing power for stability.
Example: Hopper-v2¶
Currently, we have implemented the H-term into several widely-used DRL algorithms, PPO, SAC, TD3, and DDPG. Here, we present the performance on a benchmark problem Hopper-v2 using PPO algorithm.
The implementations of PPO+H in here
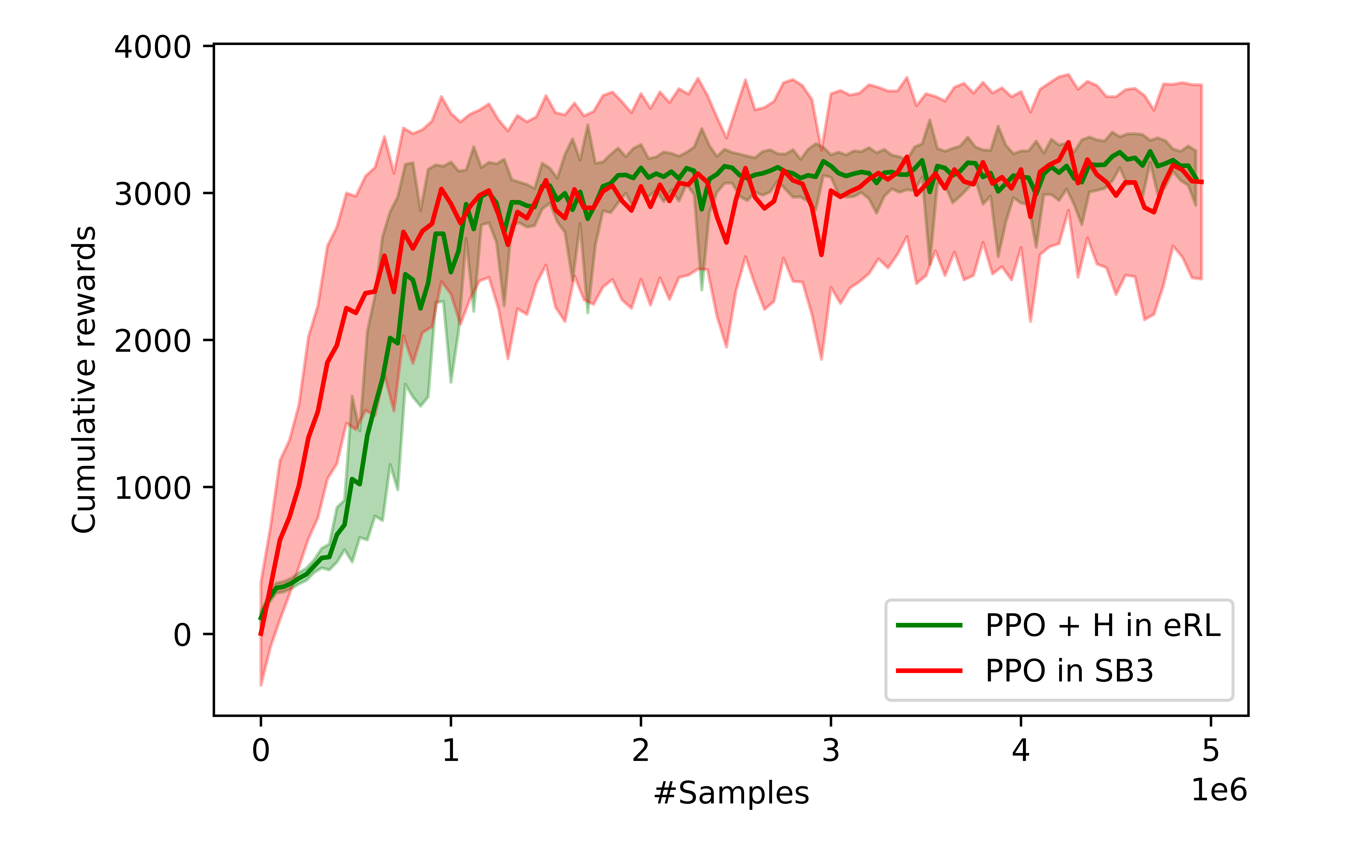
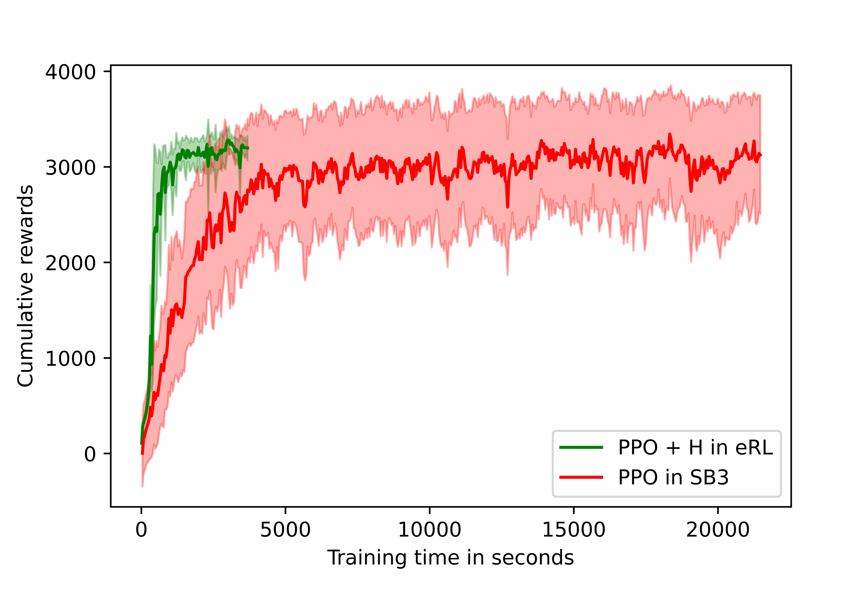
In terms of variance, it is obvious that ElegantRL substantially outperforms Stable-Baseline3. The variance over 8 runs is much smaller. Also, the PPO+H in ElegantRL completed the training process of 5M samples in about 6x faster than Stable-Baseline3.